Lab 1 Notes and Hacks
void merge(int arr[], int l, int m, int r)
{
// Find the sizes of two subarrays to be merged
int n1 = m - l + 1;
int n2 = r - m;
/* Create temp arrays */
int[] L = new int[n1];
int[] R = new int[n2];
/* Copy data to temp arrays */
for (int i = 0; i < n1; ++i)
L[i] = arr[l + i];
for (int j = 0; j < n2; ++j)
R[j] = arr[m + 1 + j];
/* Merge the temp arrays */
// Initial indexes of first and second subarrays
int i = 0, j = 0;
// Initial index of merged subarray array
int k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
// MISSING CODE #1 (need to keep the left on the left side and the right on the right side if left is less than or equal to right)
arr[k] = L[i];
i++;
}
else {
// MISSING CODE #2 (need to swap the left and right subarrays if left is greater than right)
arr[k] = R[j];
j++;
}
k++;
}
/* Copy remaining elements of L[] if any */
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
/* Copy remaining elements of R[] if any */
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
import java.util.Arrays;
public class MergeSort {
public static void main(String[] args) {
String[] values = {"pranavi", "natalie", "prisha", "divya", "dylan", "lily"};
mergeSort(values, 0, values.length - 1);
System.out.println("Our Scrum Team Members' Names Are: " + Arrays.toString(values));
}
public static void mergeSort(String[] a, int from, int to) {
if (from == to) {
return;
}
int mid = (from + to) / 2;
// sort the first and the second half
mergeSort(a, from, mid);
mergeSort(a, mid + 1, to);
merge(a, from, mid, to);
}
public static void merge(String[] a, int from, int mid, int to) {
int n = to - from + 1; // size of the range to be merged
String[] b = new String[n]; // merge both halves into a temporary array b
int i1 = from; // next element to consider in the first range
int i2 = mid + 1; // next element to consider in the second range
int j = 0; // next open position in b
// as long as neither i1 nor i2 past the end, move the smaller into b
while (i1 <= mid && i2 <= to) {
if (a[i1].compareTo(a[i2]) < 0) {
b[j] = a[i1];
i1++;
} else {
b[j] = a[i2];
i2++;
}
j++;
}
// copy any remaining entries of the first half
while (i1 <= mid) {
b[j] = a[i1];
i1++;
j++;
}
// copy any remaining entries of the second half
while (i2 <= to) {
b[j] = a[i2];
i2++;
j++;
}
// copy back from the temporary array
for (j = 0; j < n; j++) {
a[from + j] = b[j];
}
}
}
MergeSort.main(null);
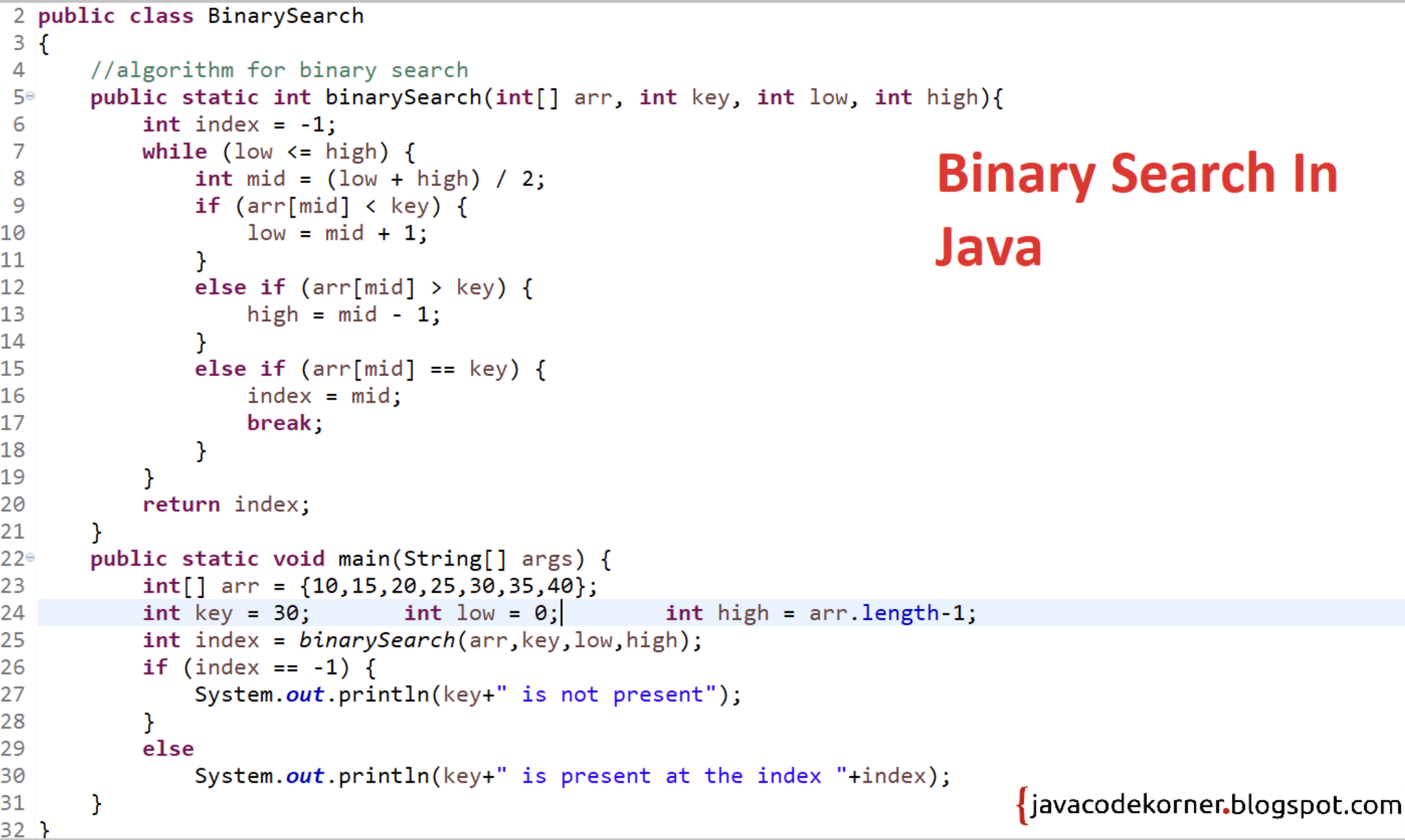
Topic 2 - Binary Search
Binary Search
- searching algorithm used by repeatedly dividing search interval by half
- one of the fastest searching methods
Questions
- Which of the following is a prerequisite for using binary search in Java?
- The array must be sorted in ascending order
- What is the worst-case scenario for binary search in Java?
- The element being searched for is not in the array
- Which of the following data structures is best suited for binary search?
- Array
- What is returned if the target is not present in the array?
- False
- What is returned if the target is present multiple times in the array?
- The index of one of the occurrences will be returned
Hacks and Homework
Binary Search Hack #1
- Given an int array[] = {1, 3, 5, 7, 9, 23, 45, 67}, search the number 45 and give it's index with Binary search, BUT do this using recursion. Make sure to include informative comments to explain the code as you write the algorithm.
public class BinarySearchRecursive {
public static int binarySearch(int arr[], int start, int end, int target) {
if (end >= start) {
// finding the middle of the array
int mid = start + (end - start) / 2;
if (arr[mid] == target) {
return mid;
// if the number at the middle of the array is greater than the target number, it searches left half of the array
} else if (arr[mid] > target) {
return binarySearch(arr, start, mid - 1, target);
// otherwise it searches the right side of the array
} else {
return binarySearch(arr, mid + 1, end, target);
}
}
return -1;
}
public static void main(String args[]) {
// creating the array
int arr[] = {1, 3, 5, 7, 9, 23, 45, 67};
// setting what number in the array the binary search is searching for
int target = 45;
int index = binarySearch(arr, 0, arr.length - 1, target);
// print statement if the target number isn't in the array
if (index == -1) {
System.out.println("Element not present in array");
// print statement if the target number is found with the index number
} else {
System.out.println("Element found at index " + index);
}
}
}
BinarySearchRecursive.main(null);
public class BinarySearch {
// merge sort method
public static void mergeSort(int[] array, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(array, left, mid);
mergeSort(array, mid + 1, right);
// merging all the sorted subarrays into one array
merge(array, left, mid, right);
}
}
// merge method
private static void merge(int[] array, int left, int mid, int right) {
// creating a temporary array to be same length as input array
int[] temp = new int[array.length];
// copies the values of the elements in the range left to right of the input array to the corresponding indices in temp
for (int i = left; i <= right; i++) {
temp[i] = array[i];
}
// initializes three variables i, j, and k
int i = left;
int j = mid + 1;
int k = left;
// compares temp[i] and temp[j], assigns the smaller value to array[k], increments i, j, and k based on the smaller value until either i or j reaches its boundary
while (i <= mid && j <= right) {
if (temp[i] <= temp[j]) {
array[k] = temp[i];
i++;
} else {
array[k] = temp[j];
j++;
}
k++;
}
// if i is less than or equal to mid, copies remaining elements in the left subarray to its proper position in array
while (i <= mid) {
array[k] = temp[i];
k++;
i++;
}
}
// binary search method
public static int binarySearch(int[] array, int left, int right, int target) {
if (right >= left) {
// finding the middle of the array and setting it as "mid"
int mid = left + (right - left) / 2;
if (array[mid] == target) {
return mid;
// if the number at the middle of the array is greater than target number, searches left half of array
} else if (array[mid] > target) {
return binarySearch(array, left, mid - 1, target);
// otherwise, searches right half of array
} else {
return binarySearch(array, mid + 1, right, target);
}
}
return -1;
}
// main method
public static void main(String[] args) {
// making the array
int[] array = {5, 6, 3, 1, 8, 9, 4, 7, 2};
// sorting the array
mergeSort(array, 0, array.length - 1);
// setting the target number in the array
int target = 7;
int index = binarySearch(array, 0, array.length - 1, target);
// print statement if the target number isn't found
if (index == -1) {
System.out.println("Element not found");
// print statement if the target number is found with the index number
} else {
System.out.println("Element found at index " + index);
}
}
}
BinarySearch.main(null);